Corrigé 2010

Détails

Catégorie : géométrie plane

1. Soit M un point du plan.pan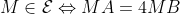  
 

 

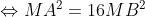
Faisons intervenir les barycentre  et  des  systèmes  et respectives. 
Alors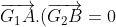  

E est donc le  cercle de diamètre 
L'ensemble F est l'arc capable d par les points A, B et l'angle .
Soit T l'unique demi droite d'origine  telle que pour tout point P de T, on a :
signons par H l'intersection de la médiatrice de [ AB] avec la perpendiculaire à T passant par A et 
par C le cercle de centre H et de rayon HA
. Alors  est l'arc de C mit A et B tel que F et T se trouvent dans des demi plans distincts de frontière
(AB).

3.a) D étant l'image de B par l'hométhétie de centre A et de rapport , . 
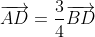On en déduit que .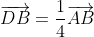
C étant l'image de B par la rotation de centre A et  d'angle 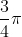 on a AC = AB et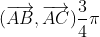 

Dans le tableau suivant les points de la deuxième ligne sont les image s par s des points  de la première
ligne.

Le rapport de s est  est son angle est modulo  : 
 
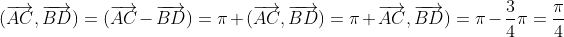
Le rapport est de  et son angle est  

b) On a aussi   = rapport de s c'est à dire = 4 ou I appartient à  
Puis  = angle de s c'est à dire  ou I appartient .

I est donc le seul point d'intersection de  et de On a encore  =  angle de s c'est à dire 



On a encore  = angle de s c'est à diere  

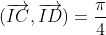
D'autre part  = - angle de s c'est à dire 

On en déduit en faisant la différence  c'est à dire 

Donc les point I,A,C et D sont cocycliques, autrement dit I appartient au cercle circonscrit au triangle ACD.

• < Précédent
• Suivant >