disciplines

Vous êtes ici : Accueil

disciplines_s2

Français

Epreuves du bac

2008 :

GEOMETRIE DANS L’ESPACE

Corrigé 2013 : solide dans l'espace

Détails: Catégorie : GEOMETRIE DANS L’ESPACE

2. $H$ appartient bien à la sphère de diamètre $[AS]$ car le triangle $AHS$ est rectangle en $H$ .

3. Puisque $M$ appartient au cercle $\mathcal{C}$ de diamètre $[AB]$ , $(MB)$ est perpendiculaire à $(AM).$

De plus, $\Delta=(AS)$ étant perpendiculaire au plan $\mathcal{P}$ est orthogonale à toute droite de ce plan, en particulier à $(BM).$

La droite $(BM)$ étant orthogonale à $(AM)$ et $(AS)$ , est orthogonale au plan $(AMS)$ défini par ces deux droites.

On en déduit que $(BM)$ est orthogonale à toute droite de ce plan, en particulier à $(AH).$

Comme par hypothèse $(AH)$ est perpendiculaire à $(MS)$ , $(AH)$ est orthogonale au plan $(BMS)$ défini par les deux droites $(BM)$ et $(MS)$ .

4. $(AH)$ étant orthogonale au plan $(BMS)$ est orthogonale à $(BS)$ et par hypothèse $(AI)$ est perpendiculaire à $(BS)$ ; par conséquent $(AHI)$ est le plan passant par $I$ et perpendiculaire à la droite $(BS)$ c'est à dire $(\Pi)$ : $H$ appartient bien à $(\Pi)$ .

$A$ appartient à $(\Sigma)$ par hypothèse.

5. a. $I$ appartient à $(\Sigma)$ car le triangle $AIS$ est rectangle en $I$ .

D'après la question 2, $H$ appartient à $(\Sigma)$ .

Donc l'intersection de $(\Sigma)$ et de $(\Pi)$ est le cercle passant par les points $A, I$ et $H$ , lequel est le cercle de diamètre $[AI]$ . En effet $(AH)$ étant perpendiculaire au plan $BMS,$ est orthogonale à toute droite de ce plan, en particulier à $(HI)$

b. $H$ appartenant à $(\Sigma)$ et à $(\Pi)$ appartient à leur intersection $\Gamma$ .

c 2017 :

Détails: Catégorie : GEOMETRIE DANS L’ESPACE

1. A(0, 0, 0), B(1, 0, 0), C(1, 1, 0), D(0, 1, 0), E(0, 0, 1), F(1, 1, 0), G(1, 1, 1), H(1, 0, 1)

a. Le vecteur $\overrightarrow{BD}\,=\,\overrightarrow{AD}-\overrightarrow{AB}$ a pour coordonnées (-1, 1, 0) c’est à dire $\overrightarrow{BD}\,=-\,\vec{i}+\vec{j}$

Le vecteur $\overrightarrow{BG}\,=\,\overrightarrow{AG}-\overrightarrow{AB}$ a pour coordonnées (0, 1, 1) c’est à dire $\overrightarrow{BD}\,=\,\vec{j}+\vec{k}$

Donc $\overrightarrow{BD}\wedge\overrightarrow{BG}\,=\,(-\vec{i}+\vec{j})\wedge(\vec{j}+\vec{K})\,=\,-\vec{k}+\vec{j}+\vec{i}$ . Les coordonnées de $\overrightarrow{BD}\wedge\overrightarrow{BG}$ sont (1, 1,-1).

b. Le plan (BGD) peut être défini comme le plan passant par B et de vecteur normal
$\vec{n}\,=\,\overrightarrow{BD}\wedge\overrightarrow{BG}$ . Un point P de coordonnées (x, z, y) appartient donc à ce plan si et seulement si $\vec{n}.\overrightarrow{BP}\,=\,0$ c’est à dire 1(x - 1) + 1(y - 0) - 1(z - 0) = 0 ou x + y - z - 1 = 0.

Cette dernière équation est donc une équation cartésienne de (BGD).

c. On a $\overrightarrow{EC}\,=\,\vec{n}$ qui est normal au plan (BGD), donc la droite (EC) est bien perpendiculaire au plan (BGD).

2. La distance du point C au plan (BGE) est $r\,=\,\frac{|x_c+y_c-z_c-1|}{\sqrt{1^2+1^2+1^2}}\,=\,\frac{\sqrt{3}}{3}$ .

Un point P de coordonnées (x, z, y) appartient donc à la sphère S si et seulement si $CP^2\,=\,r^2$ c’est à dire

$(x-1)^2+(y-1)^2+(z-0)^2\,=\,\frac{1}{3}\; ou\;(x-1)^2+(y-1)^2+z^2\,=\,\frac{1}{3}$ . Cette dernière équation est donc une équation cartésienne de S.

3. A tout $\alpha$ appartenant à l’intervalle [0, 1] on associe le point M de coordonnées $(\alpha,\alpha,1-\alpha)$ .

a. Pour que M soit un point du segment [EC], il faut et il suffit qu’il soit barycentre de ces deux points avec des poids positifs de somme 1.

cherchons donc $t\in[0,1]$ tel que $\overrightarrow{AM}\,=\,(1-t)\overrightarrow{AE}+\overrightarrow{tAC}$ c'est à dire
$\alpha,\alpha,1-\alpha\,=\,(1-t)(0,0,1)+t(1,1,0)\,=\,(t,t,1-t)$
Donc $t\,=\,\alpha$ .

b. Les points E et C appartiennent au plan médiateur du segment [BD] ; donc ce plan contient la droite (EC) et partant le point M : MBD est un triangle isocèle en M. La distance

$d(\alpha)$ de M à cette droite est donc égale à MO,O étant le milieu de [BD]. Les coordonnées de O sont (1/2, 1/2, 0).

$d(\alpha)\,=\,MO\,=\,\sqrt{\left(\alpha-\frac{1}{2}\right)^2+\left(\alpha-\frac{1}{2}\right)^2+(1-\alpha-0)^2}\,=\,\sqrt{3\alpha^2-4\alpha+\frac{3}{2}}$

c.

Pour que la distance de M à la droite (BD) soit mini-
male il faut et il suffit que la fonction d ait un minimum.
$d^{\prime}(x)\,=\,\frac{3\alpha-2}{d(\alpha)}$ . Voici le tableau de variations de d.

Pour que la distance soit minimale il faut et il suffit que

$\alpha$ soit égal à 2/3.

La distance minimale est alors égale à $\sqrt{1/6}$ et les coordonnées de L sont $\left(\frac{2}{3},\;\frac{2}{3},\;\frac{1}{3}\right)$

d. Le centre de gravité du triangle BGD a pour coordonnées
$\frac{1}{3}(x_B+x_G+x_D,y_B+y_G+y_D,z_B+z_G+z_D)\,=\,\frac{1}{3}(2,2,1)=$ coordonnées de L.

Le centre de gravit´e de BGD est bien L.

4. a. Soit P un point de coordonnées (x, y, z) et P' un point de coordonnées (x', y', z').
$\begin{array}{lll}P^{\prime}=h(P)&\Leftrightarrow&\overrightarrow{EP^{\prime}}=\alpha\overrightarrow{EP}\\\\&\Leftrightarrow&(x^{\prime},y^{\prime},z^{\prime}-1)=\alpha(x,y,z,-1)\\\\&\Leftrightarrow&\left\{\begin{array}{lll}x^{\prime}&=&\alpha x\\\\y^{\prime}&=&\alpha y\\\\z^{\prime}&=&\alpha z+1-\alpha|\end {array}\right.\end{array}$

Ce dernier système est l’expression analytique de h.

b. Posons h(C) = C'. D’après la question précédente, C' a pour coordonnées :

$(k\,x_c,k\,y_c,z_c+1-k)\,=\,(k,k,1-\alpha)$ = coordonnées de M;

donc M = C' = h(C).

c. S' est la sphère de centre h(C) = M et de rayon |k|r. Un point P de coordonnées (x, z, y) appartient donc à la sphère S' si et seulement si $MP^2,=\,k^2r^2$ c’est à dire $(x-k)^2+(y-k)^2+(z-1+k)^2\,=\,\frac{1}{3}k^2$ .

Cette dernière équation est donc une équation cartésienne de S'.

Corrigé 2015 :

Détails: Catégorie : GEOMETRIE DANS L’ESPACE

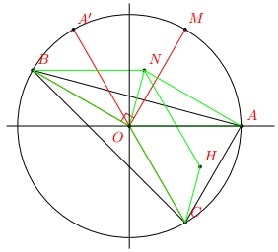
1. $A^{\prime}$ appartient C car la droite (OM) est un axe de symétrie de ce cercle. De plus $(\overrightarrow{OA},\overrightarrow{OA^{\prime}})=2(\overrightarrow{OA},\overrightarrow{OM})=2\theta[2\pi].$

C appartient C et $(\overrightarrow{OA},\overrightarrow{OC})=2\theta+\pi[2\pi].$ .

Il vient : $(\overrightarrow{OA^{\prime}},\overrightarrow{OC})=(\overrightarrow{OA^{\prime}},\overrightarrow{OA})+(\overrightarrow{OA},\overrightarrow{OC})=\pi[2\pi].$

Donc . $A^{\prime}$ et C sont bien symétriques par rapport à O.

2. a. $b=e^{i(\theta+\pi/2)}=e^{i\pi/2)}.e^{i\theta}=iz$ et $c=e^{i(2\theta+\pi)}=e^{i\pi)}.e^{2i\theta}=-z^{2}$

b. $\overrightarrow{ON}=\overrightarrow{OA}+\overrightarrow{OB}$ ; donc N est le quatrième sommet du parallèlogramme dont trois points consècutifs sont B,O et A.

$\overrightarrow{OH}=\overrightarrow{ON}+\overrightarrow{OC}$ ; donc H est le quatrième sommet du parallèlogramme dont trois points consècutifs sont C,O et N.

3. $\theta$ est différent de $\pi\2[\pi]$ signifie que z est différent de i et de -i

Alors b = iz différent de 1 (et de -1) ; A et B sont donc distincts.

De même $c=-z^{2}$ différent de 1 (et de -1) ; A et C sont donc distincts.

Enfin b - c est différent de 0 (et de -2) ; par conséquent B et C sont distincts.

$\frac{z_{\overrightarrow{AH}}}{\overrightarrow{CB}}=\frac{b+c}{b-c}\frac{iz-z^{2}}{iz+z^{2}}=\frac{1-iz}{1+iz}$ et $\frac{z_{\overrightarrow{CH}}}{\overrightarrow{BA}}=\frac{1+b}{1-b}\frac{1+iz}{1-iz}=$

Ensuite :

$\begin{array}{lll}\frac{1+iz}{1-iz}&=&\frac{1+e^{2i\alpha}}{1-e^{2i\alpha}} avec \alpha=\theta/2+\pi\/4\\\\&=&\frac{e^{-i\alpha}+e^{i\alpha}}{e^{-i\alpha}-e^{i\alpha}}\\\\&=&\frac{cos\alpha}{sin\alpha}i\textrm{ est bien imaginaire pur}\end{array}$

On en déduit que les angles $(\overrightarrow{AH},\overrightarrow{CB})$ et $(\overrightarrow{CH},\overrightarrow{BA})$ sont droits ; H est donc l’intersection des hauteurs c’est à dire l’orthocentre du triangle ABC.

a. Le discriminant de l’équation est $i^{2}+4=3$ . Les racines de l’équation sont donc

$z_{1}\frac{i+\sqrt{3}}{2}=e^{i\pi/6}$ et $z_{1}\frac{i+\sqrt{3}}{2}=e^{5i\pi/6}$

Le centre de gravité G du triangle ABC est $\frac{1}{3}(1 + b + c)$ .

Pour que H coincide avec G il faut et il su?t que 1 + b + c soit égale à $\frac{1}{3}(1 + b + c)$ c’est à dire que 1 + b+ c = 0 ou {tex}z^{2}

- iz -1 = 0{/tex}. Donc H coincide avec G si et seulement si $\theta=\pi/6$ ou $\theta=5\pi/6$

4. Puisque l’affxe z s’écrit $cos\theta + isin\theta$ , celle de H s’écrit :

$\begin{array}{lll}1 + iz - z^{2}&=&1+(cos\theta + isin\theta)-(cos\theta + isin\theta)^{2}\\&=&1-sin\theta + icos\theta-cos2\theta - isin2\theta)\textrm{formule de Moivre}\\&=&1-sin\theta -cos2\theta+i(cos2\theta - sin2\theta)\end{array}$

Donc H est le point de H de paramètre $\theta$ .

Sous-catégories

EXAMEN.SN V2.0 © RESAFAD SENEGAL Creative Commons License - Avenue Bourguiba x rue 14 Castors, Dakar (Sénégal) - Tél/Fax : +221 33864 62 33