terminales.examen.sn

Vous êtes ici : Accueil

Corrigé 2018 :

Détails: Catégorie : géométrie plane

1. $A^\prime = f(A)$ a pour affixe $z_{A^\prime}=e^{i|z_A|}z_A=e^{i\pi}\pi=-\pi=-z_A.$ .
B^\prime = f(B) a pour affixe $z_{B^\prime}=e^{i|z_B|}z_B=e^{2i\pi}2\pi=2\pi=-z_B.$ .

2. Le point O est invariant par f. Un point M distinct de O, d’affixe z est invariant par f si et seulement si $e^{|z|}z=z\quad et\quad z\neq O.$ .

$\begin{matrix}&e^{|z|}z&=&z\\\Leftrightarrow&e^{|z|}&=&1\\\Leftrightarrow&|z|&=&2k\pi,k\in\mathbb{N}^\ast\\\Leftrightarrow&OM&=&2k\pi,k\in\mathbb{N}^\ast\end{matrix}$

E est donc l’ensemble des cercles de centre O et de rayon $2k\pi,k\in\mathbb{N}$

3. L’affixe $z_c$ de C est $2e^{i\pi\slash 3}}$ . Un point M d’affixe z appartient à $\Delta$ si et seulement si z et $z_c$ ont même argument c’est à dire si et seulement si $ae^{i\pi\slash 3}$ , a avec a réel > 0

Un point M(z) de $\Delta$ et son image M^\prime(z^\prime) sont symétriques par rapport à si et seulement si $z^\prime=\bar{z}$ .

$\begin{array}{llll}&\bar{z}&=&e^{i|z|}z\\\\\Leftrightarrow&ae^{i\pi\slash 3}&=&ae^{i|z|}e^{i\pi\slash 3}(On\;pourrait\; remplacer\; |z| par\; a)\\\\\Leftrightarrow&e^{-2i\pi\slash 3}&=&e^{i|z|}\\\\\Leftrightarrow&\exists k\in\mathbb{N}^\ast,|z|&=&-2\pi\slash 3+2k\pi\end{array}$

4. a. $\mathcal{C}_k=\mathcal{C,2k\pi}$ .

$a_k=\pi[2(k+1)\pi]^2-\pi(2k\pi)^2=\pi^3(8k+4)$ .

b. La suite $a_n$ est la suite arithmétique de premier terme $a_1=12\pi^2$ et de raison $8\pi^3$ .

c. $\lim_{n\to}a_n==\infty$ .

5. a. M(z) appartient à $Delta$ et est symétrique avec son image par rapport $(O,\vec{u})$ si et seulement s’il existe $k^\prime\in\mathbb{N}^\ast$ tel que $|z|=-2\pi\slash 3+2k^\prime\pi$ . Donc un point M(z) appartient à $(\Delta)\cap\mathcal{D}_k$ et est symétrique avec son image par rapport $(O,\vec{u})$ si et seulement s’il existe $k^\prime\in\mathbb{N}^\ast$ tel que :

$\left\{\begin{array}{lll}|z|&=&-\frac{2\pi}{3}+2k^\prime\pi\\\\2k\pi&\leq&|z|\leq(k+1)\pi\end{array}\right.\Leftrightarrow\left\{\begin{array}{lll}|z|&=&-\frac{2\pi}{3}+2k^\prime\pi\\\\2k\pi&\leq&\frac{2\pi}{3}+2k^\prime\pi\leq2(k+1)\pi\end{array}\right.$

$\Leftrightarrow\left\{\begin{array}{lll}|z|&=&-\frac{2\pi}{3}+2k'\pi\\\\k&+&\frac{1}{3}\leq k'\leq k+1+\frac{1}{3}\end{array}\right.\Leftrightarrow\left\{\begin{array}{lll}|z|&=&-\frac{2\pi}{3}+2k^\prime\pi\\\\k^\prime&=&k+1\end{array}\right. Donc$

$z =2\pi\left(k+\frac{2\pi}{3}\right)e^{i\pi\slash 3}$

b. Soit M(z) un point de $\mathcal{D}_k$ et M^\prime(z^\prime) son image par f.
Alors |z^\prime| = |z| puisque $z^\prime=e^{i|z|}z$ .

Donc si |z| est compris entre $2k\pi$ et , il en est de même de |z^\prime|. Autrement dit si M
appartient à $\mathcal{D}_k$ , son image appartient à $\mathcal{D}_k$ .

Corrigé 2010

Détails: Catégorie : géométrie plane


1. Soit M un point du plan.pan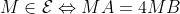

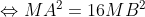
Faisons intervenir les barycentre  et  des  systèmes  et respectives. 
Alors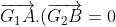  

E est donc le  cercle de diamètre 
L'ensemble F est l'arc capable d par les points A, B et l'angle .
Soit T l'unique demi droite d'origine  telle que pour tout point P de T, on a :
signons par H l'intersection de la médiatrice de [ AB] avec la perpendiculaire à T passant par A et 
par C le cercle de centre H et de rayon HA
. Alors  est l'arc de C mit A et B tel que F et T se trouvent dans des demi plans distincts de frontière
(AB).

3.a) D étant l'image de B par l'hométhétie de centre A et de rapport , . 
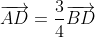On en déduit que .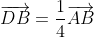
C étant l'image de B par la rotation de centre A et  d'angle 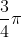 on a AC = AB et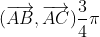

Dans le tableau suivant les points de la deuxième ligne sont les image s par s des points  de la première
ligne.

Le rapport de s est  est son angle est modulo  : 
 
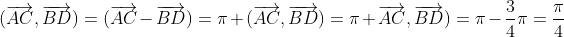
Le rapport est de  et son angle est  

b) On a aussi   = rapport de s c'est à dire = 4 ou I appartient à  
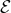
Puis  = angle de s c'est à dire  ou I appartient .

I est donc le seul point d'intersection de  et de On a encore  =  angle de s c'est à dire 



On a encore  = angle de s c'est à diere

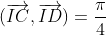
D'autre part  = - angle de s c'est à dire

On en déduit en faisant la différence  c'est à dire 

Donc les point I,A,C et D sont cocycliques, autrement dit I appartient au cercle circonscrit au triangle ACD.

corrigé 2013 : vecteurs

Détails: Catégorie : géométrie plane

1. Puisque $m=x+ix, m-i =x+i(x-1) = i(x-1-ix) = i\ \overline{m-1}.$

Donc { $|m-i|=|i|\ |m-1|= |m-1| =\sqrt{x^2+(x-1)^2}$

$(m-i)\ (m-1) = i\ \overline{m-1}(m-1)=i\ |m-1|\ ^2$ est bien imaginaire pur.

$m(1+i)=x(1+i)^2= 2ix$ est bien imaginaire pur.}

$O(0), I(1),K(1+i),J(i).$

2. a. Le rapport de $s$ est $k=\dfrac{JM}{JO}=\dfrac{|m-i|}{1}=|m-i|.$

Puisque $I$ et $M$ ont pour images respectives $I'$ et $M'$ par $s$ , on a : $k=\dfrac{I'M'}{IM}=\dfrac{I'M'}{|m-1|}$ ; donc { $I'M'=|m-1||m-i|$ .}

b. Le rapport de $s\circ s$ est $k^2= |m-i|^2.$

$J$ et $O$ ont pour images respectives $J$ et $s\circ s(O)=s(M)=M'$ par $s\circ s$ .

On a donc : $\dfrac{JM'}{JO} =\mbox{rapport de } s\circ s=|m-i|^2$ ; donc $JM'=JO |m-i|^2= |m-i|^2$ .

c. D'après la première question on a :

{ $I'M'=|m-1||m-i| = |m-i|^2=JM'.$ }

3. a. Le centre de $s$ étant le point $J(i),$ l'écriture complexe de $S$ est $z'=a(z-i)+i$ , $a$ nombre complexe à déterminer. $O$ a pour image $M(m)$ se traduit par : $m=a(-i)+i$ ; donc $a=(i-m)/i=1+im$ ; donc $z'=(1+im)(z-i)+i$ et

l'écriture complexe de $S$ est : $z'=(1+im)z+m.$

$I'$ a pour affixe $(1+im)\times 1+m= m(1+i)+1$ .

$K'$ a pour affixe $(1+im) ( 1+i)+m= 1+i +im$ .

$M'$ a pour affixe $(1+im)m +m= m(2+im)$ .

Par conséquent :

Le vecteur $\overrightarrow{II'}$ a pour affixe $z_{I'}-z_I = m(1+i)+1-1$

{Le vecteur $\overrightarrow{II'}$ a donc pour affixe $=m(1+i)$ }

Le vecteur $\overrightarrow{M'I'}$ a pour affixe $z_{I'}-z_{M'} = m(1+i)+1-m(2+im) = -i m^2+(-1+i)m +1 = i\big(m^2-(1+i)m -1\big)= -i(m-i)(m-1)$ .

{Le vecteur $\overrightarrow{M'I'}$ a donc pour affixe $-i(m-i)(m-1)$ . }

Puisque $m(1+i)$ est imaginaire pur, le vecteur $\overrightarrow{II'}$ est un directeur de la droite $(IK)$ ;

{le point $I'$ appartient donc à la droite $(IK)$ .}

4. Puisque $(m-i)(m-1)$ est imaginaire pur, $i(m-i)(m-1)$ est réel pur,

{le vecteur $\overrightarrow{M'I'}$ est donc orthogonal de la droite $(IK)$ .}

On en déduit que le point $I'$ est bien le projeté orthogonal de $M'$ sur $(IK)$ .

a. La relation (\ref{EqParabole}) devient $M'J=d\big(M', (IK)\big)$ .

Donc { $M'$ appartient à la parabole de foyer $J$ et de directrice la droite $(IK)$ .}

Corrigé 2012

Détails: Catégorie : géométrie plane

1. $A$ étant le symétrique de $F$ par rapport à $(D),$ on a $d(A,F) = 2 d(A, D)$ , le point $A$ est donc sur $(\mathcal{H})$ ; et comme la droite $(AF)$ est perpendiculaire à $(D)$ , $A$ est un sommet de $(\mathcal{H})$ .

Soit $H$ le milieu du segment $[FA]$ . Les points $F,A', H$ et $A$ appartiennent à une même perpendiculaire à $(D)$ .

Un point $M$ est un sommet de $(\mathcal{H})$ ssi il appartient à l'axe focal i.e à la droite $(FH)$ et $FM = 2 HM$ .

Cette dernière relation signifie que $\overrightarrow{FM}^2= 2^2\overrightarrow{HM}^2$ ou
$(\overrightarrow{FM} -2 \overrightarrow{HM})(\overrightarrow{FM} +2 \overrightarrow{HM})=0$ .

Les deux vecteurs $\overrightarrow{FM}-2\overrightarrow{HM}$ et $\overrightarrow{FM}+2\overrightarrow{HM}$ sont donc orthogonaux et puisqu'ils sont colinéaires, un de ces deux vecteurs est nul (et l'autre non nul).

Comme $\overrightarrow{FA}=2\overrightarrow{HA}$ , on doit avoir $\overrightarrow{FA'} = -2\overrightarrow{HA'}$ ; donc
$\begin{array}{llll} \overrightarrow{FA'} &=&2\overrightarrow{A'F}+ 2\overrightarrow{FH} &\\ &=&2\overrightarrow{A'F}+ \overrightarrow{FA} &\mbox{car } H\mbox{ est le milieu de } [F A] \end{array}{tex}$

Par conséquent $\overrightarrow{FA'}=\dfrac13 \overrightarrow{FA}$

$\overrightarrow{AA'} = \overrightarrow{AF}+ \overrightarrow{FA'} = -\overrightarrow{FA} +\dfrac 13\overrightarrow{FA}= \dfrac 23 \overrightarrow{FA}$

Le point $\Omega$ est le milieu du segment $[AA '].$

La construction des asymptotes n'est pas demandée. (Leur réunion a pour équation $(x-a)^2-\dfrac13(3y-b)^2 =0$ dans le repère de l'exercice avec $F(a, b)$ )

2.a. Un point $M$ du plan d'affixe $z = x+iy$ appartient à $(\mathcal{C})$ si et seulement si $OM = OF$ c'est à dire $|z| = |a|$ ou $z \bar z =a \bar a$

Un point $M$ du plan d'affixe $z = x+iy$ appartient à $(\mathcal{H})$ si et seulement si $AF = 2\ d(M,D)$ c'est à dire $|z-a| =2 |y|$ ou $(z -a)( \bar z - \bar a )=4 \Big[\dfrac 1{2 i}(z -\bar z)\Big]^2$ .

Finalement $M$ appartient à $(\mathcal{H})$ ssi $(z -a)( \bar z - \bar a ) + (z -\bar z) ^2 =0$ .

b. Un point $M$ du plan d'affixe $z$ appartient à $(\mathcal{C}) \cap (\mathcal{H})$ ssi
$\left\{\begin{array}{lll} z\bar z - a\bar a &=&0\\ (z-a) (\bar z-\bar a)+(z-\bar z)^2 &=&0\\ \end{array}\right.$

Dans la première relation, tirons $\bar z$ en fonction de $z$ , mettons cette valeur dans la deuxième relation, multiplions par $z^2$ et développons; alors
$M$ appartient à $(\mathcal{C}) \cap (\mathcal{H})$ ssi
$\left\{\begin{array}{lll} z\bar z - a\bar a &=&0\\ z^4 -\bar a z^3 -a^2\bar a z +a^2\bar a^2 &=&0\\ \end{array}\right.$

Puisque le point $A$ dont l'affixe est $\bar a$ appartient à
$(\mathcal{C}) \cap (\mathcal{H})$ , $\bar a$ est solution de chacune des deux équations. On peut donc mettre $z-\bar a$ en facteur dans le polynôme $z^4 -\bar a z^3 -a^2\bar a z +a^2\bar a^2$ comme le suggère la question posée.

En procédant par identification ou par division euclidienne, on trouve $z^4 -\bar a z^3 -a^2\bar a z +a^2\bar a^2 = (z-\bar a)(z^3-a^2\bar a)$ par conséquent
$\begin{array}{lll } M \in (\mathcal{C}) \cap (\mathcal{H}) &\Leftrightarrow & \left\{\begin{array}{lll} z \bar z - a\bar a &=&0\\ (z-\bar a)(z^3-a^2\bar a)&=&0\\ \end{array}\right. \end{array}$

On peut donc prendre $k = a^2\bar a$

c. Puisque $k = a^2\bar a,\; |k| = |a|^3 = r^3,\; \arg k = \arg (a^2) + \arg (\bar a )= 2\theta-\theta =\theta$ et $k = r^3\mbox{ e}^{i\theta}$

$\bar a$ est une solution de l'équation $z-\bar a$ .

L'équation $z^3-a^2\bar a = 0$ est équivalente à $z^3 = r ^3 \mbox{e}^{i\theta}$ soit $z = r \mbox{e}^{i(\theta+2\ell \pi)/3},\; \ell \in \Z$ .

Cette équation a donc trois solutions : $z_1 = r \mbox{e}^{i \theta /3},\; z_2= r \mbox{e}^{ i(\theta+2 \pi) /3}$ et $z_3 =r \mbox{e}^{ i(\theta+4 \pi) /3 }$
et comme pour tout $p \in \set{1, 2,3},\; z_p\bar z_p = r^2 = a\bar a$ , les trois complexes $z_p$ sont bien solutions du système.

Pour montrer que les points $M_p$ ayant pour affixes les $z_p$ forment un triangle équilatéral il suffit de vérifier que $\dfrac{z_1-z_2}{z_1-z_3} = \mbox{e}^{i\pi/3}$ ou $\mbox{e}^{-i\pi/3}$

$\dfrac{z_1-z_2}{z_1-z_3} = \dfrac{\mbox{e}^{i \theta /3} -\mbox{e}^{i(\theta+2 \pi )/3 }}{\mbox{e}^{i \theta /3}-\mbox{e}^{i(\theta+4 \pi) /3 }} = \dfrac{1 -\mbox{e}^{2i \pi /3 }}{1-\mbox{e}^{ 4i \pi /3 }} = \dfrac{\mbox{e}^{i\pi/3}}{\mbox{e}^{2i\pi/3}}\dfrac{\mbox{e}^{-i\pi/3} -\mbox{e}^{ i \pi /3 }}{\mbox{e}^{-2i\pi/3}-\mbox{e}^{ 2i \pi /3 }}= \mbox{e}^{-i\pi/3}\; \dfrac{2i\sin(\pi /3)} {2i\sin(2\pi /3)}=\mbox{e}^{-i\pi/3}$

Remarque 1.

1. Lorsque l'on prend comme origine $O$ l'intersection de $(FA)$ et de $(D)$ , alors $\arg F =\pi/2$ ou $-\pi/2$ et $A$ est confondu avec l'un des $M_p$

2. Les trois complexes $z_p$ vérifient $z_1 = z_1 . 1,\;z_2 = z_1 j$ et $z_2 = z_1 j^2$ avec $j =\mbox{e}^{2 i\pi/3}$ .

$N_1, N_2$ et $N_3$ étant les points d'affixes respectives $1, j, j^2$ , le triangle $M_1M_3M_3$ est l'image du triangle $N_1N_3N_3$ par la similitude de centre $O$ de rapport $|z_1|=r$ et d'angle $\arg z_1 = \theta/3.$

Puisque le triangle $N_1N_3N_3$ est équilatéral, il en est de même du triangle $M_1M_3M_3$ .

Corrigé 2008 : transformations et simitude

Détails: Catégorie : géométrie plane

1.a. Le point $P '$ est tel que

$f(P)=t\circ r(P)=t(P)=P '$ .

Donc le point $P '$ est entièrement défini par la relation $\overrightarrow{PP} '=\overrightarrow{JQ}$ ;

$P '$ est tel que $JPP 'Q$ soit un parallélogramme.

Le point $Q '$ est tel que

$f(Q)=t\circ r(Q)=t(R)=Q '$ .

Donc le point $Q '$ est entièrement défini par la relation $\overrightarrow{RQ} '=\overrightarrow{JQ}$ ;

$Q '$ est tel que $JQQ 'R$ soit un parallélogramme.

La droite $(IJ)$ est une droite des milieux pour le triangle $PQR$ , donc $JIR$ a même nature que $PQR$ :

$JIR$ est équilatéral direct

La droite $(JQ)$ est la médiatrice du segment $[P,R]$ parce que le triangle $PQR$ est équlatérale. Donc, puisque $J$ est le milieu de $[Q,Q_1]$ , l'image $PQ_1R$ du triangle équilatérale direct $PQR$ par la symétrie orthogonale d'axe $(PR)$ est un triangle équilatérale indirect.

$r$ est la rotation de centre $P$ et d'angle $(\overrightarrow{PQ},\overrightarrow{PR})=\dfrac{\pi}{3}$ . Donc $r(R)=Q_1$ .

Ensuite, $f(R)=t\circ r(R)=t(Q_1) = J\Rightarrow \boxed{f(R)=J}$ .

On sait que $f=t\circ r$ est une rotation de même angle que $r$ = $\dfrac{\pi}{3}$ .

La relation $f(R)=J$ et $JIR$ est équilatéral direct entraîne que le centre de $f$ est $I$ .

$f$ est la rotation de centre $I$ et d'angle $\dfrac{\pi}{3}$

On en déduit, puisque $f(P) = P '$ que {le triangle $IPP '$ est équilatéral direct}.

2. Antécédent $\Omega$ $J$ $R$ $I$

Image par $s$ $\Omega$ $P$ $I$ $P '$

a. L'angle de $s$ est $(\overrightarrow{JR}, \overrightarrow{PI})=(\overrightarrow{PJ}, \overrightarrow{PI})$ L'angle de $s$ est $-\dfrac{\pi}{6}$

Le rapport de $s$ est $\dfrac{PI}{JR}$ . Or $PI=PR\cos \dfrac{\pi}{6}=2JR\dfrac{ \sqrt{3}}{2}$ . Donc le rapport de $s$ est $\sqrt{3}$ .

On a $(\overrightarrow{RI },\overrightarrow{IP}')=(\overrightarrow{IQ},\overrightarrow{IP} ')=(\overrightarrow{IQ},\overrightarrow{IP})+(\overrightarrow{IP },\overrightarrow{IP} ')=-\dfrac{\pi}{2}+\dfrac{\pi}{3}=-\dfrac{\pi}{6}$ angle de $s$ .

$\dfrac{IP '}{RI}=\dfrac{IP}{RI}=\sqrt{3}$ rapport de $s$ .

Les trois conditions:

$\left\{ \begin{array}{lll} s(R) & = & I \\ (\overrightarrow{RI },\overrightarrow{IP}')&=&\textrm{angle de}\; s\\ \dfrac{IP '}{RI}&=& \textrm{rapport de}\; s \end{array} \right.$ suffisent pour dire que $s(I)=P '$

b. Puisque les similitudes planes directes conservent les angles, on peut lire dans le tableau précédent que:
angle de $s$ = $(\overrightarrow{\Omega R},\overrightarrow{\Omega I}) = (\overrightarrow{J R}, \overrightarrow{P I})$ .

Or $(\overrightarrow{J R}, \overrightarrow{P I}) = (\overrightarrow{PR}, \overrightarrow{P I})$ parce que le point $J$ appartient au segment $[P,R]$ .

Donc $(\overrightarrow{\Omega R},\overrightarrow{\Omega I}) = (\overrightarrow{PR}, \overrightarrow{P I})$

et comme les quatre points $\Omega,R, P$ et $I$ ne sont pas alignés, ils sont cocycliques.

De même $-\dfrac{\pi}{6}$ = angle de $s$ = $(\overrightarrow{\Omega J},\overrightarrow{\Omega P})$ .

D'un autre côté, la droite $(Q_1J)$ étant la bissectice du triangle équilatérale indirect $PQ_1R$ , l'angle $(\overrightarrow{Q_1J},\overrightarrow{Q_1 P})$ vaut $-\dfrac{\pi}{6}$ .

On en déduit que $(\overrightarrow{\Omega J},\overrightarrow{\Omega P})=(\overrightarrow{Q_1J},\overrightarrow{Q_1 P})$ puis que les points $\Omega,J, P$ et $Q_1$ sont cocycliques

En résumé, le point $\Omega$ appartient à l'intersection des deux cercles $C_1$ et $C_2$ ; où $C_1$ est le cercle contenant les points $P,I$ et $R$ et $C_2$ le cercle contenant les points $P,J$ et $Q_1$ .

De plus le point $\Omega$ est différent de $P$ parce que $\Omega$ est fixé par $s$ et $P$ non.

Ces conditions définissent parfaitement le point $\Omega$

Plus d'articles...

EXAMEN.SN V2.0 © RESAFAD SENEGAL Creative Commons License - Avenue Bourguiba x rue 14 Castors, Dakar (Sénégal) - Tél/Fax : +221 33864 62 33