terminales.examen.sn

Vous êtes ici : Accueil

c 2017 :

Détails: Catégorie : Interférences lumineuses

5.1.
5.1.1. $E_{ph(a)}\,=\,E_6-E_4\,=\,1,84\,eV\, ;\,E_{ph(b)}\,=\,E_6-E_3\,=\,2,82\,eV\, ;\,E_{ph(c)}\,=\,E_3-E_1\,=\,2,73\,eV\, ;\,$

5.1.2. $E_{ph}\,=\,\frac{hc}{\lambda}\Rightarrow\lambda\,=\,\frac{hc}{E_{ph}}$ .

$\lambda_a\,=\,\frac{6,62.10^{-34\times3.10^8}}{1,84\times1,6.10^{-19}}\,=\,675\,nm.\; ;\;\lambda_b\,=\,\frac{6,62.10^{-34\times3.10^8}}{2,82\times1,6.10^{-19}}\,=\,440\,nm.\; ;\;\lambda_c\,=\,\frac{6,62.10^{-34\times3.10^8}}{2,73\times1,6.10^{-19}}\,=\,455\,nm.\; ;\;$

Elles appartiennent toutes au domaine du visible.

5.2.
5.2.1. Sources cohérentes : elles présentent un déphasage constant et sont synchrones.

5.2.2.1. $S_1S_2\,=\,a\;et\; OM\,=\,x\Rightarrow O_1M\,=\,x-\frac{a}{2}\quad et\quad O_2M\,=\,x+\frac{a}{2}$

avec $a\,\prec\prec\prec D$ .

En considérant les triangles rectangles $(S_1O_1M)$ et $(S_2O_2M)$

on a : $d_1^2\,=\,D^2+\left(x-\frac{a}{2}\right)^2$ et $d_2^2\,=\,D^2+\left(x+\frac{a}{2}\right)^2\Leftrightarrow d_2^2-d_1^2\,=\,2ax\; \Rightarrow$

$(d_2-d_1)(d_2+d_1)\,=\,2ax.$

On a : $\delta\,=\,d_2-d_1$

or $a\prec\prec\prec D\Rightarrow d_2+d_1\approx 2D\Rightarrow d_2-d_1\,=\,\delta\,=\,\frac{ax}{D}$

5.2.2.2. Pour une frange sombre

$\delta\,=\,(2k+1)\frac{\lambda_1}{2}\,=\,\frac{a.x}{D}\Rightarrow x\,=\,(2k+1)\frac{\lambda_1D}{2a}\Rightarrow x\,=\,\left(K+\frac{1}{2}\right)\frac{\lambda_1D}{a}.$

5.2.2.3 Pour une frange brillante

$x\,=\,k\frac{\lambda_1D}{a}\quad or\quad d\,=\,x_5-x_3\Rightarrow d\,=\,\frac{5\lambda_1D}{a}+\left(2+\frac{1}{2}\right)\frac{5\lambda_1D}{a}\,=\,\frac{15.\lambda_1.D}{2a}\Rightarrow$ .

$\lambda_1,=\,\frac{2.a.d}{15.D}\quad A.N:\quad\lambda_1\,=\,\frac{2\times 2.10^{-3}\times 1,024.10^{-3}}{15\times 486.10^{-3}}\,=\,562\,nm$

5.3.

5.3.1. $X_1\,=\,\frac{k_1\lambda_1D}{a}\quad et\quad x_2\,=\,\frac{k_2\lambda_2D}{a}.$ .Il y a coincidence pour $x_1\,=\,x_2\,=\,\Rightarrow k_1\lambda_1\,=\,k_2\lambda_2\Rightarrow\frac{k_1}{k_2}\,=\,\frac{\lambda_2}{\lambda_1}\,=\,1,5$

$\Rightarrow\frac{k_1}{k_2}\,=\,\frac{3}{2}\Rightarrow$ première coïncidence si

$k_1\,=\,3k_2\,=\,2\Rightarrow l_1\,=\,x_1\,=\,\frac{3\lambda_1D}{a}\,=\,409,7.10^{-6}m$ .

5.3.2. Extinction totale si

$x_1\,=\,x_2(2k_1+1)\frac{\lambda_1D}{2a}\,=\,x_2(2k_2+1)\frac{\lambda_2D}{2a}\Rightarrow\frac{2k_1+1}{2k_2+1}\,=\,\frac{\lambda_2}{\lambda_1}\,=\,\frac{3}{2}\Rightarrow k_1\,=\,\frac{3}{2}k_2+\frac{1}{4}$

Si l’une des valeurs $k_1$ ou $k_2$ est entière, l’autre ne peut pas l’être ; par conséquent on ne peut pas
observer une extinction totale sur l’écran.

Corrigé 2015 :

Détails: Catégorie : Interférences lumineuses

5.1.1. Expression de la longueur d’onde.

$\Delta E=E_{p}-E_{n}=hv\Longrightarrow-\frac{E_{0}}{p^{2}}+\frac{E_{0}}{n^{2}}=hv \Longrightarrow\frac{hc}{\lambda}=\frac{E_{0}}{p^{2}}-\frac{E_{0}}{n^{2}}\Longrightarrow\frac{1} {\lambda}=\frac{E_{0}}{hc.}\big(\frac{1}{p^{2}}-\frac{1}{n^{2}}\big)$

en posant = $R_{H}=\frac{E_{0}}{hc}\rightarrow\frac{1}{\lambda}=R_{H}\big(\frac{1}{p^ {2}}-\frac{1}{n^{2}}\big).$

5.1.2 Calcul de $R_{H}=\frac{E_{0}}{hc}=\frac{136\ast 1610^{-19}}{66210^{-34}\ast 3010^ {8}}=1,10.10^{7m^{-1}}$ .

5.1.3. La longueur d’onde la plus petite et la fréquence correspondante :

$\lambda_{min}$ correspond au passage de $n\infty$ à p = 1

$\frac{1}{\lambda}=R_{H}.\big(\frac{1}{p^{2}}-\frac{1}{n^{2}}\big)\Rightarrow\frac{1}{\lambda_{min}}=R_{H}\Rightarrow\lambda_{min}=\frac{1}{R_{H}}91nm$ et $Y_{max}= \frac{C}{\lambda_{min}}=3,3.10^{15}Hz$

5.1.4. Energie d'ionisation :

$\Delta E=E_{n}-E_{p}=-E_{0}.\big(\frac{1}{n^{2}}-\frac{1}{p^{2}}\big)$

L' ionisation correspond au passage de p = 1 à n $n\rightarrow\infty$

$\Rightarrow\Delta E=E_{0}=13,6eV$

5.2.1 Les niveaux de départ

$\frac{1}{\lambda_i}=R_{H}.\big(\frac{1}{n^{2}}-\frac{1}{p^{2}}\big)$ s p = 2 on a

$\frac{1}{\lambda_i}=R_{H}.\big(\frac{1}{n^{2}}-\frac{1}{4}\big)\Longrightarrow$ d où l on tire le calcul de n

$\Rightarrow$ $\left\{\begin{array}{lll}pour&\lambda_{1}&\textrm{le niveau de depart est n = 4}\\pour&\lambda_{2}&\textrm{le niveau de depart est n = 5}\end{array}\right.$

5.2.2 La longueur d'onde la plus petite.

$\lambda_min$ passage de $n\rightarrow\infty$ à p = 2

$\frac{1}{\lambda_min}=R_{H}.\big(\frac{1}{2^{2}}-0\big)\Longrightarrow\frac{1}{\lambda_min}= \frac{R_H}{4}\Rightarrow\lambda_{min}=\frac{4}{R_H}=364nm$

5.3.1 Le photon suceptible d être absorbé

Pour $\lambda_{3} = 102,6$ nm on a : $E_{photon=\lambda_{3} =12,1 eV$ $< E_{ionisation}$ ; $\Longrightarrow$ l'énergie du photon de longueur d’onde $\lambda_{3}$ est insuffisante pour ioniser l'atome d'hydrogène pris à l'état fondamental sous l action du photon de D’autre part le photon sera absorbé par l’atome d’hydrogène pris dans son état fondamental si son énergie $\big(\frac{hc}{\lambda_{3}}\big)$ est égale la variation entre l’énergie de l’état fondamental ( $E_{1}= -E_0 )$ et l’un des niveaux d’énergie permis de l’atome $\big(E_{n}=-\frac{E_{0}}{n^{2}}\big)$ .

$\frac{hc}{\lambda_{3}}=\Delta E=E_{n}-E_{1=}E=E_{n}-E_{0}\Longrightarrow E_{n}=\frac{hc}{\lambda_{3}}=E_{0}\Longrightarrow\frac{E_{0}}{n^{2}}=\frac{hc}{\lambda_{3}}-E_{0}=12,1-13,6=-1,5eV$

$\Longrightarrow n=3$ le photon correspondant à la radiation de longueur $\lambda_{3}$ est susceptible d’être absorbé par l’atome d’hydrogène pris à l’état fondamental.

Pour $\lambda_{3}=100,9$ nm un calcul analogue au précédent conduit au résultat suivant :

$E_{n} = -13,6 + 12,3 = -1,3 eV$ $\Longrightarrow n=3,2$ ; cette valeur ne correspond pas à un entier naturel.
Le photon correspondant à la longueur $\lambda_{4}$ ne peut pas être absorbé par l’atome.
Par ailleurs l’énergie du photon (12,3 eV) est insuffisante pour ioniser l’atome pris dans son état fondamental..

5.3.2 $E_{photon}14,6 eV$ > $E_{ionisation}$ . Il y a ionisation de l'atome.

Corrigé 2012 : Etude d'un dispositif de young

Détails: Catégorie : Interférences lumineuses

5-1.
5-1-1. Observation sur l’écran

On observe des segments alternativement brillants et sombres représentant des franges d’interférences..

5-1-2. Expression de la différence de marche $\delta =d_{2}-d_{1}$ .

Considérons les triangles rectangles $S_{2}HM$ et $S_{1}HM$ :

$d_{2}^{2}=D^{2}+\left(x+\frac{a}{2}\right)^{2}$

$d_{1}^{2}=D^{2}+\left(x-\frac{a}{2}\right)^2$

$d_{2}^{2} - d_{1}^{2} = (d_{2} - d_{1})(d_{2} + d_{1})=2ax \Longrightarrow \delta (d_{2} + d_{1})=2ax$

x et a $<< D \Longrightarrow d_{2}+d_{1}\approx 2D\Longrightarrow\delta =\frac{ax}{D}$

5-1-3. Déduction de l’expression de l’interfrange i et calcul de $\lambda$

Franges brillantes $\delta =k\lambda= \frac{ax}{D} \Longrightarrow x = \frac{k\lambda D}{a}$ d'où pour deux franges brillantes consécutives :

$i=x_{2} - x_{1} = \frac{(k+1)\lambda D}{a} - \frac{k\lambda D}{a} = \frac{\lambda D}{a}$

On peut utliser les franges sombres.

On tire $\lambda = \frac{ia}{D}=\frac{0,579.10^{-3} \times 10^{-3}}{1} = 579 nm$

5-2.
5-2-1.
a) Aspect de l’écran au milieu O.

Cet aspect jaune est du à la superposition des couleurs verte et rouge

b) Aspects aux points $M_{1}$ et $M_{2}$

Soit l’ordre d’interférences $p=\frac{\delta}{\lambda}$

En $M_{1}$ ( $x_{1}= 0,75 mm$ ) :

- $\lambda_{1} =500 nm \Longrightarrow p=\frac{\delta}{\lambda_1} = \frac{ax_{1}}{D\lambda_{1}}=\frac{10^{-3} \times 0,75.10^{-3}}{1 \times 500.10^{-9}} = \frac{750}{500}=\frac{3}{2} \Longrightarrow$ frange obscure.

- $\lambda_{2} = 750 nm \Longrightarrow p=\frac{ax_{1}}{D\lambda_2}=\frac{10^{-3} \times 0,75.10^{-3}}{1 \times 750.10^{-9}} = 1 \Longrightarrow$ frange brillante rouge.

On déduit qu’en $M_{1}$ la frange est brillante rouge

En $M_{2}$ ( $x_{2}= 1,5 mm$ ) :

- $\lambda_{1} \Longrightarrow p=\frac{ax_{2}}{D\lambda_{1}}=\frac{10^{-3} \times 1,5.10^{-3}}{1 \times 500.10^{-9}} = 3 \Longrightarrow$ frange brillante verte.

- $\lambda_{2} = \Longrightarrow p= \frac{ax_{2}}{D\lambda_{2}}=\frac{10^{-3} \times 1,5.10^{-3}}{1 \times 750.10^{-9}} = 2 \Longrightarrow$ frange brillante rouge.

On déduit qu’en $M_{2}$ la frange est brillante jaune.

5-2-2. Distance minimale où il y a extinction totale de la lumière.

Frange obscure $\delta = \frac{(2k+1)\lambda }{2} = \frac{ax}{D} \Longrightarrow x = \frac{(2k+1)\lambda D}{2a}$

$x_{1} = x_{2} \Leftrightarrow \frac{(2k_{1}+1)\lambda_{1} D}{2a} =\frac{(2k_{2}+1)\lambda_{2} D}{2a} \Longrightarrow (2k_{1}+1)\lambda_{1} = (2k_{2}+1)\lambda_{2} \Longrightarrow \frac{2k_{1}+1}{2k_{2}+1}=\frac{\lambda_{2}}{\lambda_{1}}$

$\Longrightarrow\frac{2k_{1}+1}{2k_{2}+1}=\frac{528}{560}=\frac{33}{35}\Longrightarrow 2K_{1}+1=33\Longrightarrow K_{1}=16$ et $2k_{2}+1=35\Longrightarrow k_{2}=17$ ;

$x = \frac{(2k_{1}+1)\lambda_{1} D}{2a}= \frac{35 \times 560.10^{-9} \times 1}{2 \times 10^{-3}}=9,24.10^{-3}= 9,24 mm$ .

5-3.
5-3-1. Observation sur l’écran. Explication.

Seule la frange centrale est blanche du fait de la superposition de toutes les franges brillantes des radiations. Sur le reste, les systèmes de franges sont décalés de part et d’autre de la frange centrale : deux à trois franges irisées sont observées au voisinage ; au-delà on observe un blanc d’ordre supérieur là où la plupart des radiations présentent une frange brillante.

5-3-2. Longueur d’onde des radiations éteintes

Position d’une frange obscure $x = \frac{(2k+1)\lambda D}{2a} \Longrightarrow \lambda = \frac{2ax}{(2k+1)D}$

$400.10^{-9} \leq \lambda \leq 800.10^{-9} \Leftrightarrow 400.10^{-9} \leq \frac{2ax}{(2k+1)D} \leq 800.10^{-9}\Longrightarrow$

$\frac{2ax}{800.10^{-9}D} \leq 2k+1 \leq \frac{2ax}{400.10^{-9}D} \Longrightarrow \frac{ax}{800.10^{-9}D} - \frac{1}{2}\leq k \leq \frac{ax}{400.10^{-9}D} - \frac{1}{2}\Longrightarrow$

$\frac{10^{-3} \times 1,5.10^{-3}}{1 \times 800.10^{-9}} - \frac{1}{2}\leq k \leq \frac{10^{-3} \times 1,5.10^{-3}}{1 \times 400.10^{-9}}- \frac{1}{2} \Leftrightarrow 1,375 \leq k \leq 3,25 \Longrightarrow$ k = 2 et k = 3.

- $k = 2 \Longrightarrow \lambda = \frac{2ax}{5D} = \frac{2 \times 10^{-3} \times 1,5.10^{-3}}{5 \times 1}= 6.10^{-7}$

- $k = 3 \Longongrightarrow\lambda = \frac{2ax}{7D} = 4,29.10^{-7}$

Les longueurs d’onde des radiations absentes sont $\lambda = 600 nm$ et $\lambda = 429 nm$

Corrigé 2014 : Détermination de longueurs d'onde

Détails: Catégorie : Interférences lumineuses

4.1. : Schéma du dispositif

4.2. Vibrations de $S_1$ et $S_2$ : $Y_{01} = Y_{02} = S_{0}sin\omega t$

4.2.1. Expression des vibrations au point M de l’écran.
Les vibrations en M accusent par rapport aux vibrations
de $S_1$ et $S_2$ un retard respectif de : $\left\{\begin{array}{l}t_{1}=\frac{d_{1}}{c}\\t_{2}=\frac{d_{2}}{c}\end{array}\right.$

Vibration issue de $S_{1}\rightarrow Y_{1}(M)=S_{0}sin\omega (t-\frac{d_{1}}{c})$

Vibration issue de $S_{2}\rightarrow Y_{2}(M)=S_{0}sin\omega (t-\frac{d_{2}}{c})$

4.2.2. Le coefficient $2S_{0}cos(\frac{\pi\delta}{\lambda})$ est l’amplitude de la vibration Y ; cela correspond à la valeur maximale de
Y au point considéré.

4.2.3.

a) L’intensité lumineuse E s’écrit : $E = CA^{2}= C × 4S_{0}^{2}cos^{2}( \frac{\pi\delta}{\lambda})$

or $cos^{2}x=\frac{1+cos 2x}{2}\rightarrow cos^{2}( \frac{\pi\delta}{\lambda})=\frac{1+cos\frac{2\pi\delta}{\lambda}}{2}\rightarrow 2cos^{2}( \frac{\pi\delta}{\lambda})=1+cos\frac{2\pi}{\lambda}\frac{ax}{D}=1+cos\frac{2\pi x}{i}$

avec $i=\frac{\lambda D}{a}$ d'où $E=2S_{0}^{2}C(1+cos\frac{2\pi x}{i})\rightarrow E=E_{0}+(1+cos\frac{2\pi x}{i})$ avec $E_{0}=2S_{0}^{2}C$

b) Les valeurs de E et la courbe E(x)=f(x) :

c) Du graphe on déduit :

• abscisses des points où l’éclairement est maximal dans l’intervalle considéré : x = {-i ; 0 ; i ; …}

• abscisses des points où l’éclairement est nul dans l’intervalle considéré : $x = \{{-\frac{i}{2} ; \frac{i}{2} ;\ … \}$

• distance séparant deux franges consécutives de même nature $d = x_{n+1} - x_{n} = i$

4.3.
4.3.1

$d=10i,\rightarrow d=10\lambda_{1}\frac{D}{a}\rightarrow \lambda_{1}=\frac{ad}{10D}$

A.N : $\lambda_{1}= 4,8.10^{-7}m=480 nm$

On mesure la distance correspondant à 10 interfranges au lieu de celle qui correspond à 1 interfrange pour avoir une détermination plus précise de l’interfrange. L’erreur de mesure est amoindrie.

4.3.2.
Pour la lumière de longueur d’onde $\lambda_{1}$ , au point considéré on a : $x_{a} = k\lambda_{1}$ avec k = 2

Pour la lumière de longueur d’onde $\lambda_{1}$ , , au point considéré on a : $x_{b} = (2k\prime +1)\frac{\lambda}{2}$ avec k’ = 1

$x_{a}=x_{b}\rightarrow \frac{3}{2}\lambda_{1}=2\lambda_{2}\rightarrow \lambda_{2}=\frac{4}{3}\lambda_{1}\rightarrow \lambda_{2}=640nm$

Corrigé 2008 : Expérience de Young

Détails: Catégorie : Interférences lumineuses

Vous êtes ici : Interférences lumineuses>Corrigé 2008 : Expérience de Young

1.
1.1.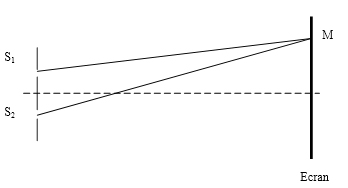

1.2. Interfrange = distance entre deux franges consécutives de même nature $i=\frac{7,6}{4}=1,9 nm$

1.3. $i=\frac{\lambda D}{a}$ on en tire $\lambda=633nm$

2. Il y a coïncidence pour la première fois à l'abscisse $X = ki_{2}=(k-1)i_{1}$

D'où $k=\frac{i_{1}}{i_{2}-i_{1}}=5$ on en tire $X = 5i_{2}=72.10^{-3}m=72$ mm

La première coincidence a lieu à 72 mm de la frange centrale.

3.1. $E_{1}-E_{0}=\frac{hC}{\lambda_{1}}$ ; on en tire $E_{1}=-3,03 eV$

de même $E_{5}-E_{1}=\frac{hC}{\lambda_{2}}$ et $E_{5}=-0,85 eV$

3.2.

On a $E_{5}-E_{0}=(E_{5}-E_{1})+(E_{1}-E_{0})$ ; de cette égalité on tire la relation suivante :

$\frac{hC}{\lamba_{0,5}}=\frac{hC}{\lamba_{0,1}}+\frac{hC}{\lamba_{1,5}}$ $\lambda_{0,5}=\frac{\lambda_{0,1}\lambda_{1,5}}{\lambda_{0,1}+\lambda_{1,5}}$

Application numérique : $\lambda_{0,5}=289,46$ nm la radiation n'appartient pas au spectre visible.

3.3.

On a $E(laser)= E_{ionise}-E_{1}+E_{c}$ d'où $Ec=E(laser)+E_{1}$ puisque $E_{ionise}=0$

$\frac{1}{2}mV^{2}= E(laser)+E_{1}$ d'où l'on tire $V = 3,5.10^{5}m.s^-1$

Plus d'articles...

EXAMEN.SN V2.0 © RESAFAD SENEGAL Creative Commons License - Avenue Bourguiba x rue 14 Castors, Dakar (Sénégal) - Tél/Fax : +221 33864 62 33